카탈란 수-대각선을 넘지 않는 경우의 수

문제

$n \times n$ 격자에서 왼쪽 아래에서 오른쪽 위 모서리로 가는 오른쪽이나 위로 가는 이동만으로 이루어진 경로를 생각하자. 이 때 왼쪽 아래와 오른쪽 위 모서리를 연결한 대각선 위로 올라가지 않는 경로는 몇 개나 있을까?

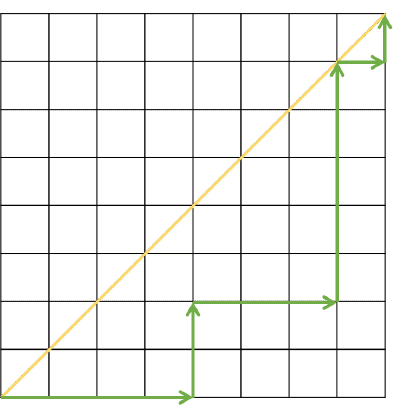
이 조건을 만족하는 경우의 수를 카탈란 수라고 하고, $C_n$으로 적습니다.

일반항

크게 두 단계에 걸쳐서 증명에 들어갑니다. 앞으로 ‘오른쪽으로 이동’을 $\Rightarrow$, ‘위로 이동’을 $\Uparrow$로 표기합니다.

대각선 조건이 없을 때

$n\times m$ 격자에서 왼쪽 아래에서 오른쪽 위 모서리로 가는 최단 경로의 개수는?

가로 길이가 $n$, 세로 길이가 $m$이기 때문에 왼쪽 아래 모서리에서 순서에 상관 없이 $\Rightarrow$을 $n$번, $\Uparrow$을 $m$번 했을 때 오른쪽 위 모서리에 도달하게 됩니다. 따라서 문제에서 묻는 최단 경로의 개수 $D_{n,m}$는 다음과 같습니다.

$D_{n,m} ={n+m \choose n} = \frac {(n+m)!}{n!m!}$

대각선 조건이 있을 때

2.1의 문제로 이 문제를 바꿀 것입니다. 핵심 아이디어는 다음과 같습니다:

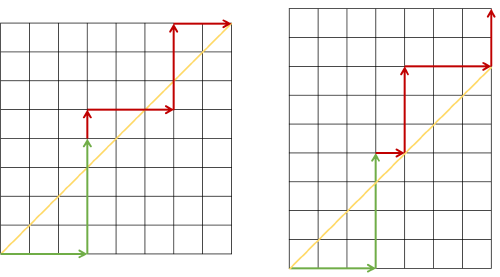
대각선을 넘어가는 경로를 생각합니다. 이 때, 대각선을 최초로 넘어간 이후의 경로를 대칭시켜버리면, $n-1 \times n+1$의 격자에서 경로를 얻을 수 있습니다. 즉, 문제의 조건을 위배하는 경로는 $n-1 \times n+1$ 격자의 경로에 대응됩니다.

그런데 그림의 $n-1 \times n+1$에 남아 있는 대각선을 살펴보면, 모든 $n-1 \times n+1$경로가 대각선을 지나갈 수밖에 없습니다. 즉, 반대로 $n-1 \times n+1$ 경로를 문제를 만족하지 않는 $n \times n$ 경로에 대응할 수 있습니다.

따라서 문제의 조건을 위배하는 경로의 개수는 $D_{n-1,n+1}$입니다.

이제 남은 것은 $n \times n$에서 모든 경로에서 조건을 위배하는 경로를 제외한 것을 세주는 것입니다!

$C_n = D_{n,n} - D_{n-1,n+1} = \frac{(2n)!}{n!n!} \left(1 - \frac {n}{n+1} \right) = \frac 1{n+1} {2n \choose n}$

이 스케치를 집합 용어를 써서 엄밀하게 적어주면 완전 증명이 됩니다.

점화식

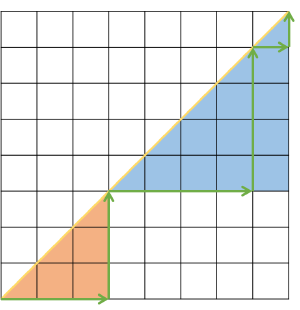
처음으로 대각선과 만나는 좌표를 중심으로 생각을 전개하면 쉽습니다. 위 그림의 경우에는 $(3,3)$에서 만나는데, 그 이후로 $(3,3)$에서 $(8,8)$로 가는 대각선을 넘지 않는 경로를 세주면 되고, 그 경우의 수는 $C_5$입니다. (대각선을 만나지 않고 끝점에 도달했더라도, 그 끝점을 대각선과 만난 점으로 생각하면 됩니다)

이제 $(0,0)$에서 $(3,3)$으로 가는 대각선과 만나지 않는 경로들을 세야 하는데, 아래 그림을 보면 역시 이미 풀었던 문제라는 것을 알 수 있습니다. 처음에 $\Rightarrow$로, 마지막에도 $\Uparrow$로 행동이 강제되는데, 그러고 남은 문제는 $2 \times 2$의 문제, 즉 $C_2$입니다.

이 셈을 $(1,1)$에서 $(8,8)$까지 모두 해서 더하면 점화식을 얻을 수 있습니다. 일반적으로 접근하면 다음과 같은 식을 쉽게 쓸 수 있습니다.

$C_n = \sum _{i=1} ^n C_{i-1} C_{n-i}$

그리고 이 점화식의 시작인 $C_0 = 1$도 같이 써주면 됩니다.