이분그래프

1. 정의

그래프 $G = (V,E)$에 대해 다음 조건을 만족하면 이분그래프bipartite graph 라고 합니다.

공집합이 아닌 $V$의 분할partition $\{V_1 ,V_2\}$가 있어서,

$E \subseteq \{ \{v_1, v_2\} : v_1 \in V_1, v_2 \in V_2 \}$

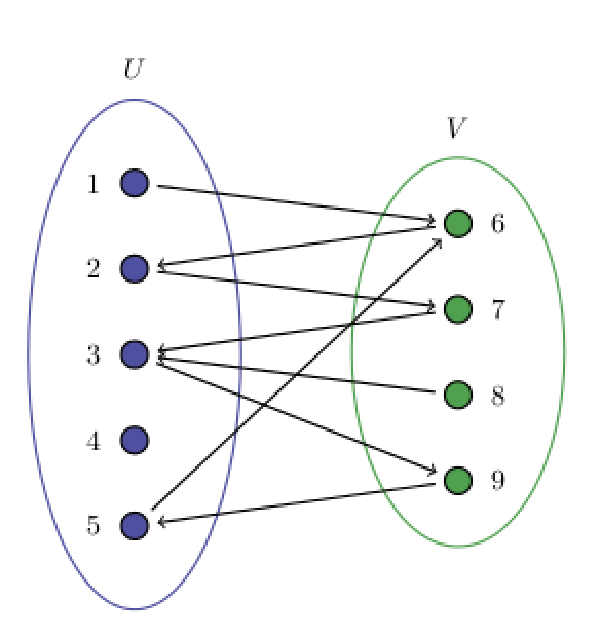
이와 같은 이분그래프에 대해 추가적인 표기법으로 $G = (V_1, V_2, E)$를 사용하기도 합니다. Figure 1과 같은 형태입니다.

2. 판별

따라서 어떤 그래프가 이분그래프인지 아닌지 판별할 때는 Figure 2와 같이 두 가지 색깔을 칠하면서 접근하면 좋습니다. 어떤 변을 잡아도 그 변을 구성하는 꼭짓점은 다른 색깔로 칠해져야 하기 때문입니다.

2.1. 알고리즘

이분그래프를 확인할 때는 BFS 방식을 사용하면 됩니다. 2에서 이분그래프를 판별하는 과정을 그대로 적용합니다. 입력 형태는 (#)와 같고, Python 3.7에서 쓰여진 코드는 다음과 같습니다:

test_nbr = int(input()) # number of test cases

def isBipartite():
    # v and e is number of vertexes and edges, respectively.
    v,e = map(int,input().split())

    # None if not colored
    # If colored, there are two bool cases: False and True.
    colorArr = [None for _ in range(v+1)]
    adjacentPoints = [[] for _ in range(v+1)]

    for i in range(e):
        v1, v2 = map(int, input().split()) # edge (v1, v2) is expected input
        adjacentPoints[v1].append(v2)
        adjacentPoints[v2].append(v1)

    queue = []
    node = set([i for i in range(1,v+1)]) # for non-connected graph

    while bool(node): # node is nonempty
        c = node.pop()
        queue.append(c)
        while bool(queue): # queue is nonempty
            start = queue[0]
            for u in adjacentPoints[start]:
                if colorArr[u] is not None:
                    if colorArr[u] is colorArr[start]:
                        return False
                else:
                    colorArr[u] = not colorArr[start]
                    queue.append(u)
            del queue[0]
            if start != c: node.remove(start)

    return True


for _ in range(test_nbr):
    print('YES' if isBipartite() else 'NO')

3. 정리

이분그래프는 홀수 길이의 순환cycle이 존재하지 않고, 그 역도 성립한다.

3.1. 정방향 증명

이분그래프는 홀수 길이의 순환이 존재하지 않는다.

이분그래프 $G = (U,V,E)$에 대해 $E \subseteq U \times V$이므로 모든 순환의 형태는 $U$와 $V$가 교대해서 나타난다. 따라서 그 순환의 길이는 짝수이다.

3.2. 역방향 증명

홀수 길이의 순환이 존재하지 않는 그래프는 이분그래프이다.

직접 색칠하면서 이분그래프를 판별할 때의 과정이 증명에 담겨있습니다. 처음에 점 하나를 잡아서 색칠해놓고, 인접한 것들을 계속 반대 색깔로 칠해 나가면서 모순이 생기는 지를 확인해야 합니다. 이를 쉽게 서술하기 위해 ‘최소 경로’라는 개념을 도입했습니다.

$G = (V,E)$에 대해 임의의 $v\in V$를 잡자. 그리고 직접 이분그래프를 설계하기 위해 다음과 같은 $A,B \subset V$를 정의한다.

$A = \{ a \in V : \text{the shortest path from } a \text{ to } v \text{ has odd length }\}\\ B = \{ b \in V: \text{the shortest path from } b \text { to } v \text{ has even length }\}$

먼저, $A \sqcup B = V$이다. ( $A,B$는 서로소disjoint이고, $A \cup B=V$라는 뜻)

이제 $E \subseteq \{ \{a,b\} : a \in A \wedge b \in B\}$임을 보일 것이다.

서로 다른 $a_1, a_2 \in A$에 대해 $a_1$과 $v$ 사이의 최소 경로 길이를 $l(a_1)$, $a_2$와 $v$ 사이의 최소 경로 길이를 $l(a_2)$라고 놓으면 다음이 성립한다:

$2 | l(a_1) + l(a_2)$

만약에 $\{a_1, a_2 \} \in E$라면 $a_1, a_2, v$를 잇는 순환의 길이가 홀수이므로 모순이다.

$B$도 이것이 똑같이 성립한다.

따라서 $A$끼리 연결된 선이 없고, $B$끼리도 연결된 선이 없으므로 $G$는 이분그래프이다.

출처

[1] https://tex.stackexchange.com/questions/15088/bipartite-graphs

[2] http://mathworld.wolfram.com/BipartiteGraph.html