쌍을 포함하는 부분구간수열의 개수 세기

2021년 5월 22일

문제

0과 1로 이루어진 수열 a가 있다. 이 수열의 부분구간수열을 a의 시작과 마지막부분에서 각각 0개 이상의 원소를 빼서 만들어지는 수열이라고 하자. 이 수열의 각 부분구간수열이 가지는 (1,1)의 쌍의 개수를 구해야 한다.

예를 들어, 수열이 [0, 1, 1, 0, 1]이라면, [1,1], [0, 1, 1], [1, 1, 0], [0, 1, 1, 0], [1, 0, 1]은 1개, [1, 1, 0, 1], [0, 1, 1, 0, 1]은 3개의 (1,1)쌍을 포함하므로, 총 11개이다.

알고리즘의 시간복잡도는 수열의 길이 N에 대해 선형이어야 한다.

풀이 1 - 인덱스에 대한 DP

모든 부분구간수열에 대해 (1,1)쌍의 개수를 세려면 부분구간수열의 총 개수가 $O(N^2)$ 이므로 요구되는 시간에 맞출 수가 없다.

$D_i$ 를 i번째 인덱스로 끝나는 각 구간에 대해 (1,1) 쌍의 개수의 총합으로 놓자. 그러면

0번째 인덱스로 끝나는 구간은 (1,1)을 포함하지 않으므로 $D_0 = 0$
$a_{i+1} = 0$ 인 경우, $D_{i+1}= D_i$ .
$a_{i+1}= 1$ 인 경우, $D_{i+1} = D_i + (x_1 + 1) + (x_2 + 1) + \cdots$ . 이 때 $\{x_1, x_2, \cdots \}$ 는 $\{a_0, a_1, \cdots, a_{i}\}$ 에서 값이 1인 원소들의 인덱스이다.

예를 들어 a가 [0, 1, 1, 0, 1]이었다면, $x_1 = 1, x_2 = 2, x_3 = 4$ 로,

$D_0 = 0$
$D_1 = D_0 = 0$
$D_2 = D_1 + (x_1 + 1) = 2$
$D_3 = D_2 = 2$
$D_4 = D_3 + (x_1 + 1) + (x_2 + 1) = 7$

따라서 각 부분구간수열이 가지는 (1,1) 쌍의 개수의 총합은 $D_0 + D_1 + \cdots + D_4 = 11$ 이다.

이 알고리즘은 $D_{i+1}$ 을 계산할 때 $a_{i+1} = 0$ 이면 바로 결과가 나오고, $a_{i+1} = 1$ 인 경우 $\sum (x_j + 1)$ 을 계산할 때 **구간 합(prefix sum)**을 이용하면 바로 결과가 나오게 할 수 있다.

#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;

int main(){
    int n;        // 입력의 길이
    cin >> n;
    int val;
    ll D[n+1];   // DP를 누적시킬 배열
    ll psum = 0;
    ll result = 0;
    for (int i=0;i<n;i++){
        cin >> val;
        if (i == 0) D[i] = 0;
        else {
            if (val == 0) D[i] = D[i-1];
            else {
                D[i] = D[i-1] + psum;
                psum += i + 1;
            }
        }
        result += D[i];
    }

    cout << result << endl;
    return 0;
}

풀이 2 - 각 (1,1) 쌍에 대해 세기

각 (1,1) 쌍에 대해 그 쌍을 포함하는 부분구간수열의 개수를 세는 방법을 생각해볼 수 있는데, 그것 또한 (1,1) 쌍의 개수가 $O(N^2)$ 이기 때문에 부족하다

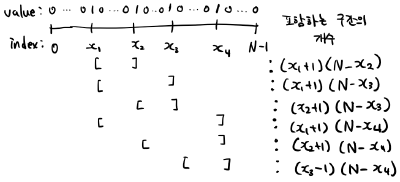
하지만 Figure 1처럼 (1,1)쌍의 두 번째 1의 인덱스가 같은 것끼리 비교하면 공통점이 보이기 시작한다. 두 번째와 세 번째는 모두 (N-x3)가 곱해지고, 네 번째부터 마지막까지는 (N-x4)가 곱해진다.

두 번째 1의 인덱스를 기준으로 개수를 세면

두 번째 1의 인덱스가 x2인 각 (1,1)에 대해 이를 포함하는 구간의 개수는 $(x_1 + 1)(N-x_2)$
두 번째 1의 인덱스가 x3인 각 (1,1)에 대해 이를 포함하는 구간의 개수는 $(x_1 +1 + x_2 + 1)(N-x_3)$
두 번째 1의 인덱스가 x4인 각 (1,1)에 대해 이를 포함하는 구간의 개수는 $(x_1 +1 + x_2 + 1+x_3+1)(N-x_4)$

이런 식으로 마지막 1에 도달할 때까지 계속 반복해서 더해나가면 된다.

각 경우에 대해 $(N-x_i)$ 는 바로 계산 가능하고, $\sum_{i=1} ^m {x_i} + m$ 은 **구간 합(prefix sum)**을 이용하면 바로 계산 가능하다.

#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;

int main(){
    int n;            // 입력의 길이
    cin >> n;
    int val;
    vector<int> m;    // 1의 인덱스를 저장하는 벡터
    for (int j=0;j<n;j++){
        cin >> val;
        if (val == 1) m.push_back(j);
    }

    ll result = 0;
    ll psum = 0;
    for (auto &it: m){
        result = result + psum * (n-it);
        psum += it+1;
    }
    cout << result << endl;
    return 0;
}